Automatic Control Knowledge Repository
You currently have javascript disabled. Some features will be unavailable. Please consider enabling javascript.Details for: "linear trajectory planning for electrical resistance"
Name: linear trajectory planning for electrical resistance
(Key: NRRYR)
Path: ackrep_data/problem_solutions/linear_trajectory_electrical_resistance View on GitHub
Type: problem_solution
Short Description:
Created: 2020-12-30
Compatible Environment: default_conda_environment (Key: CDAMA)
Source Code [ / ] solution.py
Solved Problems: controller design by using linear trajectory planning |
Used Methods: system proporty method_trajectory_planning method_trajectory_planning
Result: Success.
Last Build: Checkout CI Build
Runtime: 3.8 (estimated: 10s)
Plot:
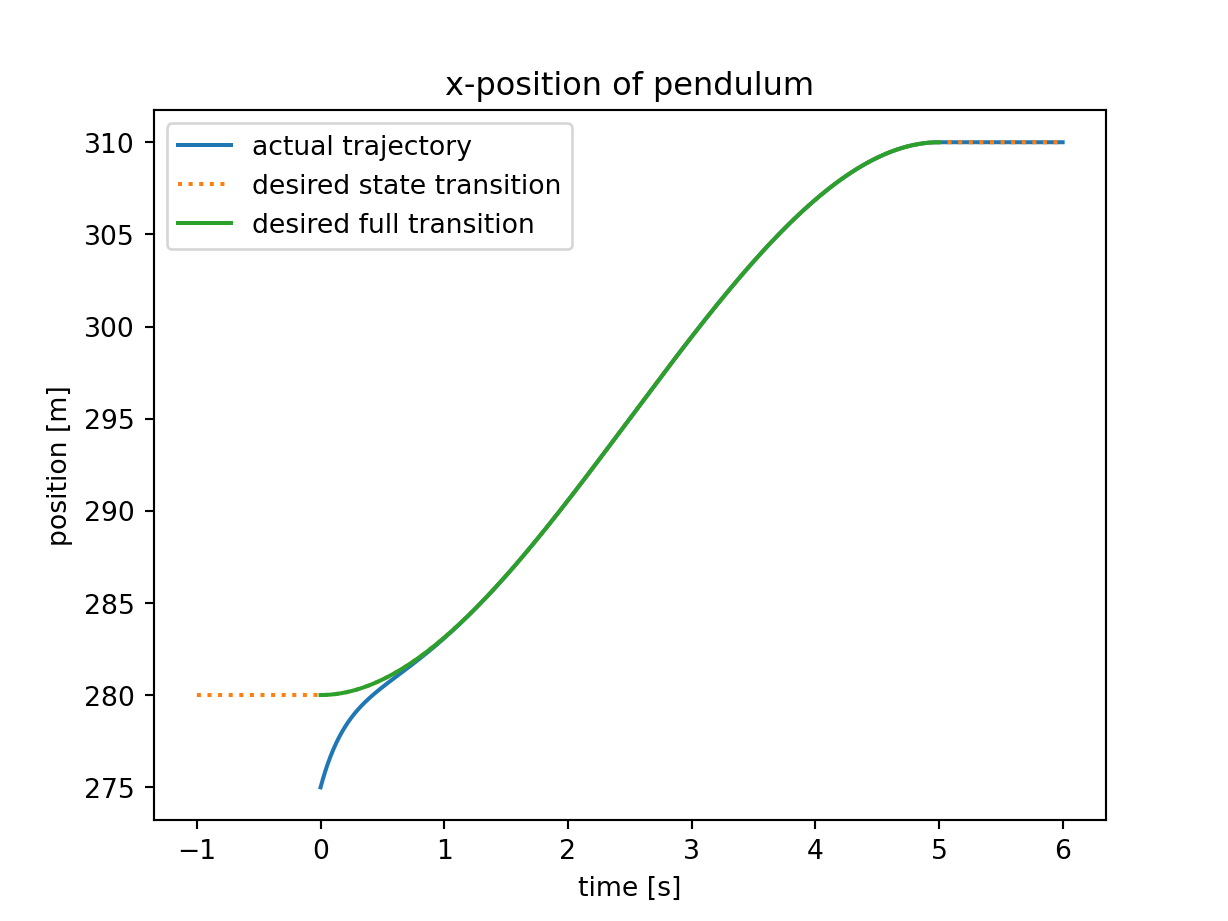
The image of the latest CI job is not available. This is a fallback image.
Path: ackrep_data/problem_solutions/linear_trajectory_electrical_resistance View on GitHub
Type: problem_solution
Short Description:
Created: 2020-12-30
Compatible Environment: default_conda_environment (Key: CDAMA)
Source Code [ / ] solution.py
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
problem solution for control problem: design a controller by using linear trajectory planning.
"""
try:
import coprime_decomposition as cd # noqa
except ImportError:
from method_packages.coprime_decomposition import coprime_decomposition as cd
import sympy as sp
import symbtools as st
import matplotlib.pyplot as plt
import method_trajectory_planning as tp # noqa
import control
from control import matlab
import os
from ackrep_core.system_model_management import save_plot_in_dir
class SolutionData:
pass
def solve(problem_spec):
s, t, T = sp.symbols("s, t, T")
# transfer function of system
transfer_func = problem_spec.transfer_func()
z_func, n_func = transfer_func.expand().as_numer_denom() # separate numerator and denominator
z_coeffs = [float(c) for c in st.coeffs(z_func, s)] # coefficients of numerator
n_coeffs = [float(c) for c in st.coeffs(n_func, s)] # coefficients of denominator
b_0 = z_func.coeff(s, 0)
# Boundary conditions for q and its derivative
q_a = [problem_spec.YA[0] / b_0, 0]
q_e = [problem_spec.YB[0] / b_0, 0]
# generate trajectory of q(t)
planer = tp.Trajectory_Planning(q_a, q_e, problem_spec.t0, problem_spec.tf, problem_spec.tt)
planer.dem = n_func
planer.num = z_func
q_poly = planer.calc_trajectory()
# trajectory of input and output
u_poly, y_poly = planer.num_den_laplace(q_poly[0])
q_func = st.expr_to_func(t, q_poly[0])
u_func = st.expr_to_func(t, u_poly) # desired input trajectory function
y_func = st.expr_to_func(t, y_poly) # desired output trajectory function
# tracking controller
# numerator and denominator of controller
cd_res = cd.coprime_decomposition(z_func, n_func, problem_spec.poles)
# open_loop k(s) * P(s)
tf_k = (cd_res.f_func * z_func) / (cd_res.h_func * n_func)
z_o, n_o = sp.simplify(tf_k).expand().as_numer_denom()
# coefficients of controller
z_coeffs_c = [float(c) for c in st.coeffs(cd_res.f_func, s)] # coefficients of numerator
n_coeffs_c = [float(c) for c in st.coeffs(cd_res.h_func, s)] # coefficients of denominator
# coefficients of open loop
z_coeffs_o = [float(c) for c in st.coeffs(z_o, s)]
n_coeffs_o = [float(c) for c in st.coeffs(n_o, s)]
# In order to simulate the closed loop system with the controller,
# the system is divided into two subsystems. one of them with the y_ref as input
# and the other with u_ref
close_loop_1 = control.feedback(control.tf(z_coeffs_o, n_coeffs_o))
close_loop_2 = control.feedback(control.tf(z_coeffs, n_coeffs), control.tf(z_coeffs_c, n_coeffs_c))
# subsystem 1 with y_ref
y_1 = control.forced_response(close_loop_1, problem_spec.tt2, y_func(problem_spec.tt2), problem_spec.x0_1)
# subsystem 2 with u_ref
y_2 = control.forced_response(close_loop_2, problem_spec.tt2, u_func(problem_spec.tt2), problem_spec.x0_2)
solution_data = SolutionData()
solution_data.u = u_func
solution_data.q = q_func
solution_data.y_1 = y_1[1]
solution_data.y_2 = y_2[1]
solution_data.y_func = y_func
save_plot(problem_spec, solution_data)
return solution_data
def save_plot(problem_spec, solution_data):
plt.figure(1) # simulated trajectory of CuZn-ball
plt.plot(problem_spec.tt2, solution_data.y_1 + solution_data.y_2, label="actual trajectory")
plt.plot(problem_spec.tt1, solution_data.y_func(problem_spec.tt1), ":", label="desired state transition")
plt.plot(problem_spec.tt, solution_data.y_func(problem_spec.tt), label="desired full transition")
plt.xlabel("time [s]")
plt.ylabel("position [m]")
plt.title("x-position of pendulum")
plt.legend(loc=2)
# save image
save_plot_in_dir()
Solved Problems: controller design by using linear trajectory planning |
Used Methods: system proporty method_trajectory_planning method_trajectory_planning
Result: Success.
Last Build: Checkout CI Build
Runtime: 3.8 (estimated: 10s)
Plot:

The image of the latest CI job is not available. This is a fallback image.