Automatic Control Knowledge Repository
You currently have javascript disabled. Some features will be unavailable. Please consider enabling javascript.Details for: "double integrator transition using PyTrajectory"
Name: double integrator transition using PyTrajectory
(Key: UKJZI)
Path: ackrep_data/problem_solutions/double_integrator_transition_with_pytrajectory View on GitHub
Type: problem_solution
Short Description:
Created: 2020-07-02
Compatible Environment: default_conda_environment (Key: CDAMA)
Source Code [ / ] solution.py
Solved Problems: double integrator transition |
Used Methods: PyTrajectory
Result: Success.
Last Build: Checkout CI Build
Runtime: 3.8 (estimated: 3s)
Plot:
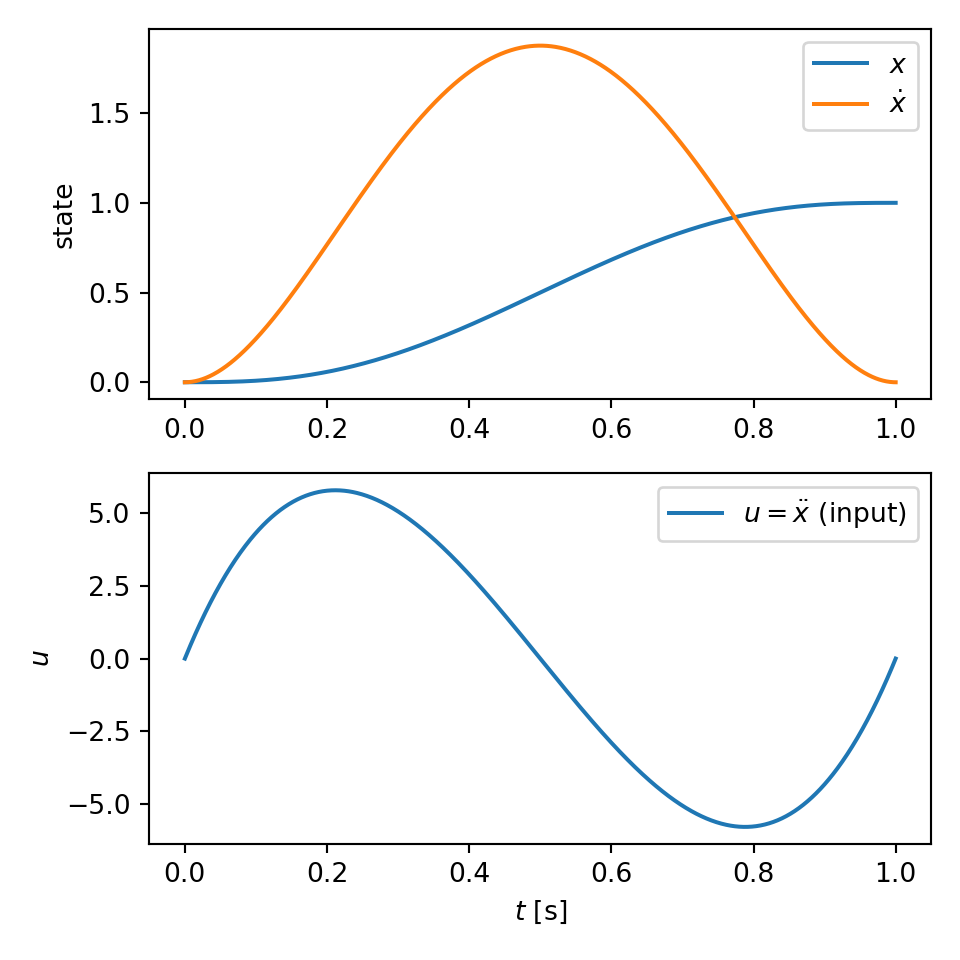
The image of the latest CI job is not available. This is a fallback image.
Path: ackrep_data/problem_solutions/double_integrator_transition_with_pytrajectory View on GitHub
Type: problem_solution
Short Description:
Created: 2020-07-02
Compatible Environment: default_conda_environment (Key: CDAMA)
Source Code [ / ] solution.py
"""
This example of the double integrator demonstrates how to pass constraints to PyTrajectory.
"""
# imports
import os
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
from ipydex import IPS
from ackrep_core.system_model_management import save_plot_in_dir
# method-specific
from pytrajectory import TransitionProblem
class SolutionData:
pass
def solve(problem_spec):
# system state boundary values for a = 0.0 [s] and b = 2.0 [s]
xa = problem_spec.xx_start
xb = problem_spec.xx_end
T_end = problem_spec.T_transition
# constraints dictionary
con = problem_spec.constraints
def f_pytrajectory(xx, uu, uuref, t, pp):
"""Right hand side of the vectorfield defining the system dynamics
This function wraps the rhs-function of the problem_spec to make it compatible to
pytrajectory.
:param xx: state
:param uu: input
:param uuref: reference input (not used)
:param t: time (not used)
:param pp: additionial free parameters (not used)
:return: xdot
"""
return problem_spec.rhs(xx, uu)
# create the trajectory object
S = TransitionProblem(f_pytrajectory, a=0.0, b=T_end, xa=xa, xb=xb, constraints=con, use_chains=False)
# start
x, u = S.solve()
solution_data = SolutionData()
solution_data.x_func = x
solution_data.u_func = u
save_plot(problem_spec, solution_data)
return solution_data
def save_plot(problem_spec, solution_data):
tt = np.linspace(0, problem_spec.T_transition, 1000)
uu = np.array([solution_data.u_func(t)[0] for t in tt])
xx = np.array([solution_data.x_func(t) for t in tt])
plt.figure(figsize=(5, 5))
ax1 = plt.subplot(211)
plt.plot(tt, xx[:, 0], label=r"$x$")
plt.plot(tt, xx[:, 1], label=r"$\dot x$")
plt.legend()
plt.ylabel("state")
plt.subplot(212, sharex=ax1)
plt.plot(tt, uu, label=r"$u = \ddot x$ (input)")
plt.ylabel(r"$u$")
plt.xlabel("$t$ [s]")
plt.legend()
plt.tight_layout()
save_plot_in_dir()
Solved Problems: double integrator transition |
Used Methods: PyTrajectory
Result: Success.
Last Build: Checkout CI Build
Runtime: 3.8 (estimated: 3s)
Plot:

The image of the latest CI job is not available. This is a fallback image.