Automatic Control Knowledge Repository
You currently have javascript disabled. Some features will be unavailable. Please consider enabling javascript.Details for: "buck converter"
Name: buck converter
(Key: DFRJY)
Path: ackrep_data/system_models/buck_converter View on GitHub
Type: system_model
Short Description: DC-DC power converter that steps down voltage on output compared to input (by increasing current)
Created: 29.08.2022
Compatible Environment: default_conda_environment (Key: CDAMA)
Source Code [ / ] simulation.py
Related Problems:
Extensive Material:
Download pdf
Result: Success.
Last Build: Checkout CI Build
Runtime: 3.2 (estimated: 10s)
Plot:
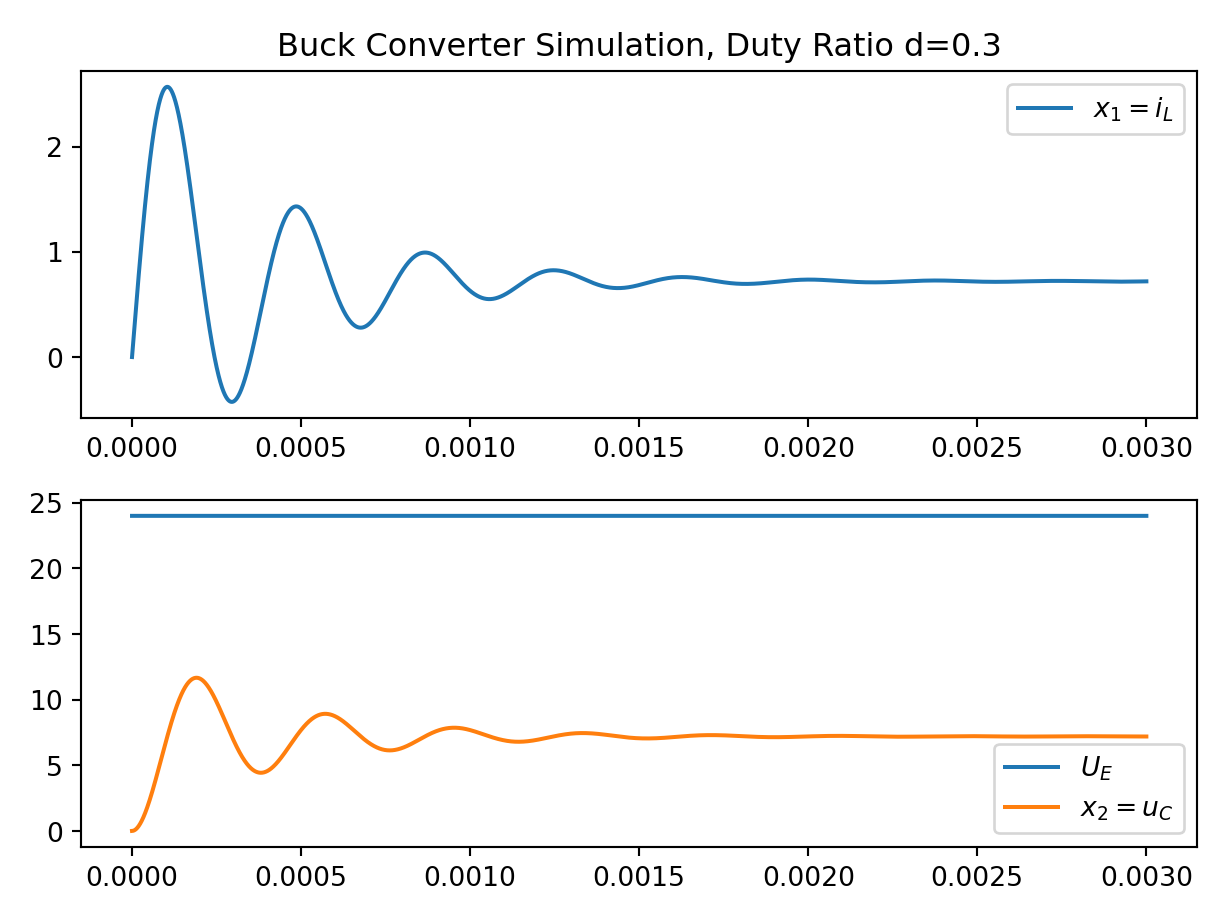
The image of the latest CI job is not available. This is a fallback image.
Path: ackrep_data/system_models/buck_converter View on GitHub
Type: system_model
Short Description: DC-DC power converter that steps down voltage on output compared to input (by increasing current)
Created: 29.08.2022
Compatible Environment: default_conda_environment (Key: CDAMA)
Source Code [ / ] simulation.py
import numpy as np
import system_model
from scipy.integrate import solve_ivp
from ackrep_core import ResultContainer
from ackrep_core.system_model_management import save_plot_in_dir
import matplotlib.pyplot as plt
import os
from ipydex import IPS
# link to documentation with examples: https://ackrep-doc.readthedocs.io/en/latest/devdoc/contributing_data.html
def simulate():
"""
simulate the system model with scipy.integrate.solve_ivp
:return: result of solve_ivp, might contains input function
"""
model = system_model.Model()
rhs_xx_pp_symb = model.get_rhs_symbolic()
print("Computational Equations:\n")
for i, eq in enumerate(rhs_xx_pp_symb):
print(f"dot_x{i+1} =", eq)
rhs = model.get_rhs_func()
# initial state values
xx0 = [0, 0]
t_end = 3e-3
tt = np.linspace(0, t_end, 10000)
simulation_data = solve_ivp(rhs, (0, t_end), xx0, t_eval=tt)
simulation_data.U_E = model.params.UE_sf
simulation_data.u = model.uu_func(0, 0)[0]
save_plot(simulation_data)
# print(simulation_data.y[:,-1])
return simulation_data
def save_plot(simulation_data):
"""
plot your data and save the plot
access to data via: simulation_data.t array of time values
simulation_data.y array of data components
simulation_data.uu array of input values
:param simulation_data: simulation_data of system_model
:return: None
"""
# ---------start of edit section--------------------------------------
# plot of your data
fig, ax = plt.subplots(2, 1)
ax[0].plot(simulation_data.t, simulation_data.y[0], label="$x_1=i_L$")
ax[0].legend()
ax[0].grid()
ax[0].set_title(f"Buck Converter Simulation, Duty Ratio d={simulation_data.u}")
ax[1].plot(simulation_data.t, np.ones_like(simulation_data.t) * simulation_data.U_E, label="$U_E$")
ax[1].plot(simulation_data.t, simulation_data.y[1], label="$x_2=u_C$")
ax[1].legend()
ax[1].grid()
ax[1].set_xlabel("Time [s]")
# ---------end of edit section----------------------------------------
plt.tight_layout()
save_plot_in_dir()
def evaluate_simulation(simulation_data):
"""
assert that the simulation results are as expected
:param simulation_data: simulation_data of system_model
:return:
"""
# ---------start of edit section--------------------------------------
# fill in final states of simulation to check your model
# simulation_data.y[i][-1]
expected_final_state = [0.71921453, 7.190941]
# ---------end of edit section----------------------------------------
rc = ResultContainer(score=1.0)
simulated_final_state = simulation_data.y[:, -1]
rc.final_state_errors = [
simulated_final_state[i] - expected_final_state[i] for i in np.arange(0, len(simulated_final_state))
]
rc.success = np.allclose(expected_final_state, simulated_final_state, rtol=0, atol=1e-2)
return rc
import sympy as sp
import symbtools as st
import importlib
import sys, os
# from ipydex import IPS, activate_ips_on_exception
from ackrep_core.system_model_management import GenericModel, import_parameters
# Import parameter_file
params = import_parameters()
# link to documentation with examples: https://ackrep-doc.readthedocs.io/en/latest/devdoc/contributing_data.html
class Model(GenericModel):
def initialize(self):
"""
this function is called by the constructor of GenericModel
:return: None
"""
# ---------start of edit section--------------------------------------
# Define number of inputs -- MODEL DEPENDENT
self.u_dim = 1
# Set "sys_dim" to constant value, if system dimension is constant
self.sys_dim = 2
# ---------end of edit section----------------------------------------
# check existence of params file
self.has_params = True
self.params = params
# ----------- SET DEFAULT INPUT FUNCTION ---------- #
# --------------- Only for non-autonomous Systems
def uu_default_func(self):
"""
define input function
:return:(function with 2 args - t, xx_nv) default input function
"""
# ---------start of edit section--------------------------------------
def uu_rhs(t, xx_nv):
"""
sequence of numerical input values
:param t:(scalar or vector) time
:param xx_nv:(vector or array of vectors) numeric state vector
:return:(list) numeric inputs
"""
D = 0.3 # duty cycle
return [D]
# ---------end of edit section----------------------------------------
return uu_rhs
# ----------- SYMBOLIC RHS FUNCTION ---------- #
def get_rhs_symbolic(self):
"""
define symbolic rhs function
:return: matrix of symbolic rhs-functions
"""
if self.dxx_dt_symb is not None:
return self.dxx_dt_symb
# ---------start of edit section--------------------------------------
x1, x2 = self.xx_symb # state components
L, C, R, U_E = self.pp_symb # parameters
u = self.uu_symb[0] # inputs
# define symbolic rhs functions
dx1_dt = -x2 / L + u * U_E / L
dx2_dt = x1 / C - x2 / R / C
# rhs functions matrix
self.dxx_dt_symb = sp.Matrix([dx1_dt, dx2_dt])
# ---------end of edit section----------------------------------------
return self.dxx_dt_symb
import sys
import os
import numpy as np
import sympy as sp
import tabulate as tab
# link to documentation with examples: https://ackrep-doc.readthedocs.io/en/latest/devdoc/contributing_data.html
# set model name
model_name = "boostconverter"
# ---------- create symbolic parameters
pp_symb = [L, C, R, U_E] = sp.symbols("L, C, R, U_E", real=True)
# ---------- create symbolic parameter functions
# parameter values can be constant/fixed values OR set in relation to other parameters (for example: a = 2*b)
L_sf = 180 * 1e-6 # uH
C_sf = 20 * 1e-6 # uF
R_sf = 10 # Ohm
UE_sf = 24 # V
# list of symbolic parameter functions
# tailing "_sf" stands for "symbolic parameter function"
pp_sf = [L_sf, C_sf, R_sf, UE_sf]
# ---------- list for substitution
# -- entries are tuples like: (independent symbolic parameter, numerical value)
pp_subs_list = []
# OPTONAL: Dictionary which defines how certain variables shall be written
# in the table - key: Symbolic Variable, Value: LaTeX Representation/Code
# useful for example for complex variables: {Z: r"\underline{Z}"}
latex_names = {U_E: r"U_E"}
# ---------- Define LaTeX table
# Define table header
# DON'T CHANGE FOLLOWING ENTRIES: "Symbol", "Value"
tabular_header = ["Symbol", "Value"]
# Define column text alignments
col_alignment = ["center", "left"]
# Define Entries of all columns before the Symbol-Column
# --- Entries need to be latex code
col_1 = ["Inductiviy", "Capacity", "Resistence", "Input Voltage"]
# contains all lists of the columns before the "Symbol" Column
# --- Empty list, if there are no columns before the "Symbol" Column
start_columns_list = [col_1]
# Define Entries of the columns after the Value-Column
# --- Entries need to be latex code
col_4 = ["H", "F", "$\Omega$", "V"]
# contains all lists of columns after the FIX ENTRIES
# --- Empty list, if there are no columns after the "Value" column
end_columns_list = [col_4]
Related Problems:
Extensive Material:
Download pdf
Result: Success.
Last Build: Checkout CI Build
Runtime: 3.2 (estimated: 10s)
Plot:

The image of the latest CI job is not available. This is a fallback image.