Automatic Control Knowledge Repository
You currently have javascript disabled. Some features will be unavailable. Please consider enabling javascript.Details for: "PVTOL with 2 forces"
Name: PVTOL with 2 forces
(Key: OHW5Z)
Path: ackrep_data/system_models/pvtol_system View on GitHub
Type: system_model
Short Description: the planar vertical take-off and landing, an underactuated nonlinear unmanned aerial vehicle
Created: 2022-05-09
Compatible Environment: default_conda_environment (Key: CDAMA)
Source Code [ / ] simulation.py
Related Problems:
PVTOL problem
Extensive Material:
Download pdf
Result: Success.
Last Build: Checkout CI Build
Runtime: 7.8 (estimated: 15s)
Plot:
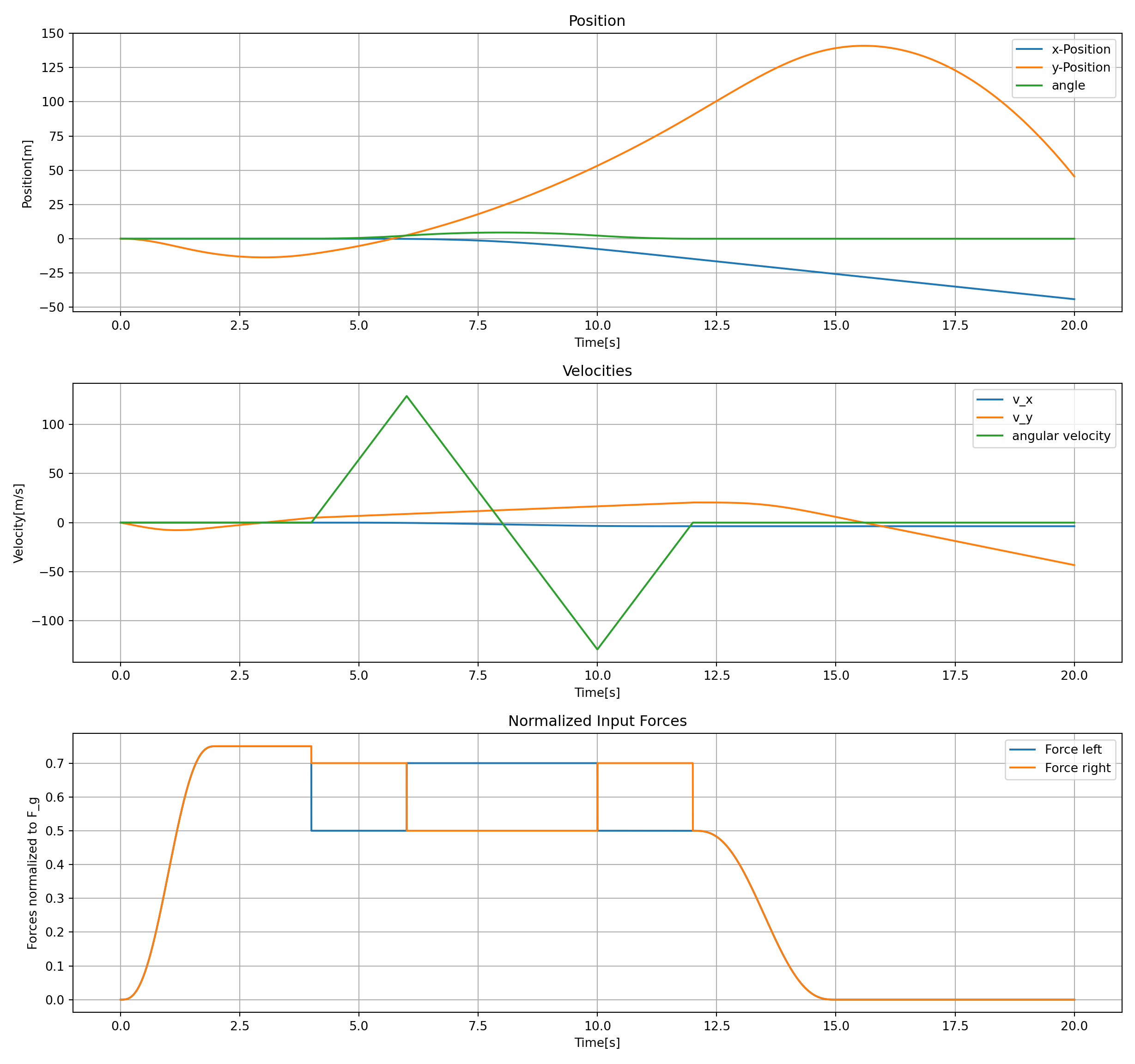
The image of the latest CI job is not available. This is a fallback image.
Path: ackrep_data/system_models/pvtol_system View on GitHub
Type: system_model
Short Description: the planar vertical take-off and landing, an underactuated nonlinear unmanned aerial vehicle
Created: 2022-05-09
Compatible Environment: default_conda_environment (Key: CDAMA)
Source Code [ / ] simulation.py
import numpy as np
import system_model
from scipy.integrate import solve_ivp
from ackrep_core import ResultContainer
from ackrep_core.system_model_management import save_plot_in_dir
import matplotlib.pyplot as plt
import os
def simulate():
model = system_model.Model()
rhs_xx_pp_symb = model.get_rhs_symbolic()
print("Computational Equations:\n")
for i, eq in enumerate(rhs_xx_pp_symb):
print(f"dot_x{i+1} =", eq)
rhs = model.get_rhs_func()
# Initial State values
xx0 = np.zeros(6)
t_end = 20
tt = np.linspace(0, t_end, 10000)
sim = solve_ivp(rhs, (0, t_end), xx0, t_eval=tt, max_step=0.01)
# if inputfunction exists:
uu = model.uu_func(sim.t, sim.y)
g = model.get_parameter_value("g")
m = model.get_parameter_value("m")
uu = np.array(uu) / (g * m)
sim.uu = uu
# --------------------------------------------------------------------
save_plot(sim)
return sim
def save_plot(simulation_data):
# create figure + 2x2 axes array
fig1, axs = plt.subplots(nrows=3, ncols=1, figsize=(12.8, 12))
# print in axes top left
axs[0].plot(simulation_data.t, np.real(simulation_data.y[0]), label="x-Position")
axs[0].plot(simulation_data.t, np.real(simulation_data.y[2]), label="y-Position")
axs[0].plot(simulation_data.t, np.real(simulation_data.y[4] * 180 / np.pi), label="angle")
axs[0].set_title("Position")
axs[0].set_ylabel("Position [m]") # y-label Nr 1
axs[0].set_xlabel("Time [s]")
axs[0].grid()
axs[0].legend()
axs[1].plot(simulation_data.t, simulation_data.y[1], label="$v_x$")
axs[1].plot(simulation_data.t, simulation_data.y[3], label="$v_y$")
axs[1].plot(simulation_data.t, simulation_data.y[5] * 180 / np.pi, label="angular velocity")
axs[1].set_title("Velocities")
axs[1].set_ylabel("Velocity [m/s]")
axs[1].set_xlabel("Time [s]")
axs[1].grid()
axs[1].legend()
# print in axes bottom left
axs[2].plot(simulation_data.t, simulation_data.uu[0], label="Force left")
axs[2].plot(simulation_data.t, simulation_data.uu[1], label="Force right")
axs[2].set_title("Normalized Input Forces")
axs[2].set_ylabel("Forces normalized to $F_g$") # y-label Nr 1
axs[2].set_xlabel("Time [s]")
axs[2].grid()
axs[2].legend()
# adjust subplot positioning and show the figure
fig1.subplots_adjust(hspace=0.5)
# fig1.show()
# --------------------------------------------------------------------
plt.tight_layout()
save_plot_in_dir()
def evaluate_simulation(simulation_data):
"""
:param simulation_data: simulation_data of system_model
:return:
"""
# fill in the final states y[i][-1] to check your model
expected_final_state = [
-44.216119976296774,
-3.680370979746213,
45.469521639337344,
-43.275661598545256,
-0.00037156407418776797,
-0.00033632680535548506,
]
# --------------------------------------------------------------------
rc = ResultContainer(score=1.0)
simulated_final_state = simulation_data.y[:, -1]
rc.final_state_errors = [
simulated_final_state[i] - expected_final_state[i] for i in np.arange(0, len(simulated_final_state))
]
rc.success = np.allclose(expected_final_state, simulated_final_state, rtol=0, atol=1e-2)
return rc
import sympy as sp
import symbtools as st
import importlib
import sys, os
from ipydex import IPS, activate_ips_on_exception # for debugging only
from ackrep_core.system_model_management import GenericModel, import_parameters
# Import parameter_file
params = import_parameters()
class Model(GenericModel):
def initialize(self):
"""
this function is called by the constructor of GenericModel
:return: None
"""
# Define number of inputs -- MODEL DEPENDENT
self.u_dim = 2
# Set "sys_dim" to constant value, if system dimension is constant
# else set "sys_dim" to x_dim -- MODEL DEPENDENT
self.sys_dim = 6
# check existance of params file
self.has_params = True
self.params = params
# ----------- SET DEFAULT INPUT FUNCTION ---------- #
# --------------- Only for non-autonomous Systems
# --------------- MODEL DEPENDENT
def uu_default_func(self):
"""
:param t:(scalar or vector) Time
:param xx_nv: (vector or array of vectors) state vector with numerical values at time t
:return:(function with 2 args - t, xx_nv) default input function
"""
m = self.get_parameter_value("m")
T_raise = 2
T_left = T_raise + 2 + 2
T_right = T_left + 4
T_straight = T_right + 2
T_land = T_straight + 3
force = 0.75 * 9.81 * m
force_lr = 0.7 * 9.81 * m
g_nv = 0.5 * self.get_parameter_value("g") * m
# create symbolic polnomial functions for raise and land
poly1 = st.condition_poly(self.t_symb, (0, 0, 0, 0), (T_raise, force, 0, 0))
poly_land = st.condition_poly(self.t_symb, (T_straight, g_nv, 0, 0), (T_land, 0, 0, 0))
# create symbolic piecewise defined symbolic transition functions
transition_u1 = st.piece_wise(
(0, self.t_symb < 0),
(poly1, self.t_symb < T_raise),
(force, self.t_symb < T_raise + 2),
(g_nv, self.t_symb < T_left),
(force_lr, self.t_symb < T_right),
(g_nv, self.t_symb < T_straight),
(poly_land, self.t_symb < T_land),
(0, True),
)
transition_u2 = st.piece_wise(
(0, self.t_symb < 0),
(poly1, self.t_symb < T_raise),
(force, self.t_symb < T_raise + 2),
(force_lr, self.t_symb < T_left),
(g_nv, self.t_symb < T_right),
(force_lr, self.t_symb < T_straight),
(poly_land, self.t_symb < T_land),
(0, True),
)
# transform symbolic to numeric function
transition_u1_func = st.expr_to_func(self.t_symb, transition_u1)
transition_u2_func = st.expr_to_func(self.t_symb, transition_u2)
def uu_rhs(t, xx_nv):
u1 = transition_u1_func(t)
u2 = transition_u2_func(t)
return [u1, u2]
return uu_rhs
# ----------- SYMBOLIC RHS FUNCTION ---------- #
# --------------- MODEL DEPENDENT
def get_rhs_symbolic(self):
"""
:return:(matrix) symbolic rhs-functions
"""
if self.dxx_dt_symb is not None:
return self.dxx_dt_symb
x1, x2, x3, x4, x5, x6 = self.xx_symb
g, l, m, J = self.pp_symb
# input
u1, u2 = self.uu_symb
# create symbolic rhs functions
dx1_dt = x2
dx2_dt = -sp.sin(x5) / m * (u1 + u2)
dx3_dt = x4
dx4_dt = sp.cos(x5) / m * (u1 + u2) - g
dx5_dt = x6 * 2 * sp.pi / 360
dx6_dt = l / J * (u2 - u1) * 2 * sp.pi / 360
# put rhs functions into a vector
self.dxx_dt_symb = sp.Matrix([dx1_dt, dx2_dt, dx3_dt, dx4_dt, dx5_dt, dx6_dt])
return self.dxx_dt_symb
import sys
import os
import numpy as np
import sympy as sp
import tabulate as tab
# tailing "_nv" stands for "numerical value"
# SET MODEL NAME
model_name = "PVTOL with 2 forces"
# CREATE SYMBOLIC PARAMETERS
pp_symb = [g, l, m, J] = sp.symbols("g, l, m, J", real=True)
# SYMBOLIC PARAMETER FUNCTIONS
# parameter values can be constant/fixed values OR set in relation to other parameters (for example: a = 2*b)
g_sf = 9.81
l_sf = 0.1
m_sf = 0.25
J_sf = 0.00076
# List of symbolic parameter functions
pp_sf = [g_sf, l_sf, m_sf, J_sf]
pp_subs_list = []
# OPTONAL: Dictionary which defines how certain variables shall be written
# in the tabular - key: Symbolic Variable, Value: LaTeX Representation/Code
# useful for example for complex variables: {Z: r"\underline{Z}"}
latex_names = {}
# ---------- CREATE BEGIN OF LATEX TABULAR
# Define tabular Header
# DON'T CHANGE FOLLOWING ENTRIES: "Symbol", "Value"
tabular_header = ["Parametername", "Symbol", "Value", "Unit"]
# Define column text alignments
col_alignment = ["left", "center", "left", "center"]
# Define Entries of all columns before the Symbol-Column
# --- Entries need to be latex code
col_1 = ["acceleration due to gravity", "distance of forces to mass center", "mass", "moment of inertia"]
# contains all lists of the columns before the "Symbol" Column
# --- Empty list, if there are no columns before the "Symbol" Column
start_columns_list = [col_1]
# Define Entries of the columns after the Value-Column
# --- Entries need to be latex code
col_4 = [r"$\frac{\mathrm{m}}{\mathrm{s}^2}$", "m", "kg", r"$\mathrm{kg} \cdot \mathrm{m}^2$"]
# contains all lists of columns after the FIX ENTRIES
# --- Empty list, if there are no columns after the "Value" column
end_columns_list = [col_4]
Related Problems:
PVTOL problem
Extensive Material:
Download pdf
Result: Success.
Last Build: Checkout CI Build
Runtime: 7.8 (estimated: 15s)
Plot:

The image of the latest CI job is not available. This is a fallback image.