Automatic Control Knowledge Repository
You currently have javascript disabled. Some features will be unavailable. Please consider enabling javascript.Details for: "stable PTn system"
Name: stable PTn system
(Key: OV6ND)
Path: ackrep_data/system_models/stable_pt_n_system View on GitHub
Type: system_model
Short Description: stable PTn element
Created: 2022-04-20
Compatible Environment: default_conda_environment (Key: CDAMA)
Source Code [ / ] simulation.py
Related Problems:
Extensive Material:
Download pdf
Result: Success.
Last Build: Checkout CI Build
Runtime: 3.8 (estimated: 10s)
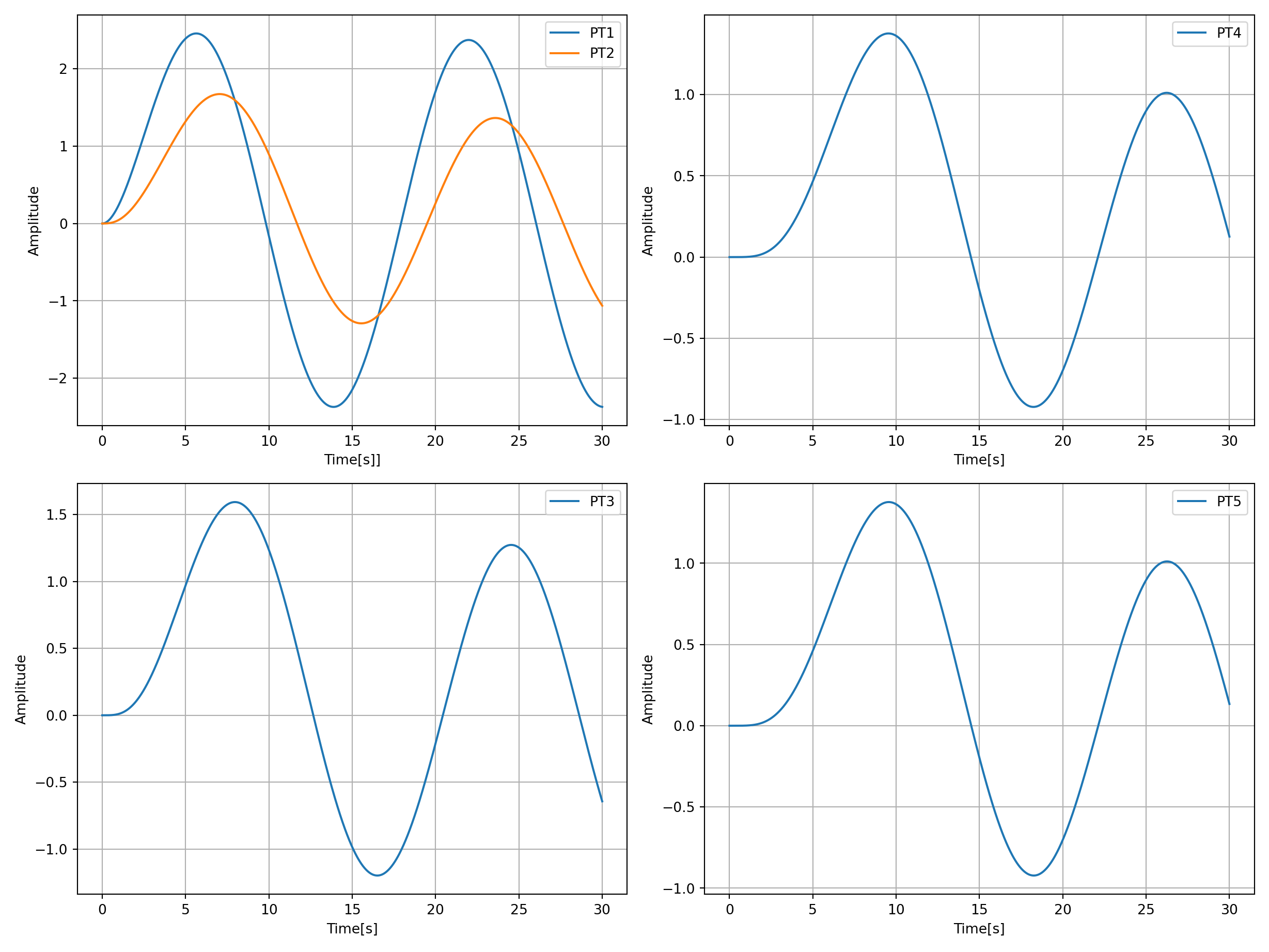
Plot:
The image of the latest CI job is not available. This is a fallback image.
Path: ackrep_data/system_models/stable_pt_n_system View on GitHub
Type: system_model
Short Description: stable PTn element
Created: 2022-04-20
Compatible Environment: default_conda_environment (Key: CDAMA)
Source Code [ / ] simulation.py
# -*- coding: utf-8 -*-
"""
Created on Mon Jun 7 19:06:37 2021
@author: Rocky
"""
import numpy as np
import system_model
from scipy.integrate import solve_ivp
from ackrep_core import ResultContainer
from ackrep_core.system_model_management import save_plot_in_dir
import matplotlib.pyplot as plt
import os
def simulate():
pp1 = [3, 2]
pp3 = [3, 5, 0.5, 1]
pp4 = [3, 5, 0.5, 1, 2]
pp5 = [3, 5, 0.5, 1, 2, 0.02]
model1 = system_model.Model(x_dim=1, pp=pp1)
model2 = system_model.Model()
model3 = system_model.Model(x_dim=3, pp=pp3)
model4 = system_model.Model(x_dim=4, pp=pp4)
model5 = system_model.Model(x_dim=5, pp=pp5)
model = [model1, model2, model3, model4, model5]
print("Simulation for PT1 to PT5 with input function u=sin(omega*t) \n")
for i in range(len(model)):
rhs_xx_pp_symb = model[i].get_rhs_symbolic()
print("Computational Equations PT" + str(i + 1) + ":\n")
for i, eq in enumerate(rhs_xx_pp_symb):
print(f"dot_x{i+1} =", eq, "\n")
# Initial State values
xx0_1 = np.zeros(1)
xx0_2 = np.zeros(2)
xx0_3 = np.zeros(3)
xx0_4 = np.zeros(4)
xx0_5 = np.zeros(5)
t_end = 30
tt = np.linspace(0, t_end, 1000)
sol1 = solve_ivp(model1.get_rhs_func(), (0, t_end), xx0_1, t_eval=tt)
sol2 = solve_ivp(model2.get_rhs_func(), (0, t_end), xx0_2, t_eval=tt)
sol3 = solve_ivp(model3.get_rhs_func(), (0, t_end), xx0_3, t_eval=tt)
sol4 = solve_ivp(model4.get_rhs_func(), (0, t_end), xx0_4, t_eval=tt)
sol5 = solve_ivp(model5.get_rhs_func(), (0, t_end), xx0_5, t_eval=tt)
sim = [sol1, sol2, sol3, sol4, sol5]
save_plot(sim)
return sim
def save_plot(sim):
# create figure + 2x2 axes array
fig1, axs = plt.subplots(nrows=2, ncols=2, figsize=(12.8, 9.6))
# print in axes top left
axs[0, 0].plot(sim[0].t, sim[0].y[0], label="PT1")
axs[0, 0].plot(sim[1].t, sim[1].y[0], label="PT2")
axs[0, 0].set_ylabel("Amplitude") # y-label
axs[0, 0].grid()
axs[0, 0].legend()
# print in axes top right
axs[1, 0].plot(sim[2].t, sim[2].y[0], label="PT3")
axs[1, 0].set_ylabel("Amplitude") # y-label
axs[1, 0].set_xlabel("Time [s]") # x-Label
axs[1, 0].grid()
axs[1, 0].legend()
# print in axes bottom left
axs[0, 1].plot(sim[3].t, sim[3].y[0], label="PT4")
axs[0, 1].grid()
axs[0, 1].legend()
# print in axes bottom right
axs[1, 1].plot(sim[4].t, sim[4].y[0], label="PT5")
axs[1, 1].set_xlabel("Time [s]") # x-Label
axs[1, 1].grid()
axs[1, 1].legend()
plt.tight_layout()
save_plot_in_dir()
def evaluate_simulation(simulation_data):
"""
:param simulation_data: simulation_data of system_model
:return:
"""
expected_final_state = [
-2.369685579668774,
-1.0626757541773422,
-0.6428946899596174,
0.12607608396072245,
0.13375873500072138,
]
rc = ResultContainer(score=1.0)
simulated_final_state = np.zeros(len(simulation_data))
for i in range(len(simulation_data)):
simulated_final_state[i] = simulation_data[i].y[0][-1]
rc.final_state_errors = [
simulated_final_state[i] - expected_final_state[i] for i in np.arange(0, len(simulated_final_state))
]
rc.success = np.allclose(expected_final_state, simulated_final_state, rtol=0, atol=1e-2)
return rc
# -*- coding: utf-8 -*-
"""
Created on Wed Jun 9 13:33:34 2021
@author: Jonathan Rockstroh
"""
import sympy as sp
import symbtools as st
import importlib
import sys, os
from itertools import combinations as comb
import numpy as np
from ipydex import IPS, activate_ips_on_exception # for debugging only
from ackrep_core.system_model_management import GenericModel, import_parameters
# Import parameter_file
params = import_parameters()
class Model(GenericModel):
def initialize(self):
"""
this function is called by the constructor of GenericModel
:return: None
"""
# Define number of inputs
self.u_dim = 1
# Adjust sys_dim to dimension fitting to default parameters
self.default_param_sys_dim = 2
# check existance of params file -> if not: System is defined to hasn't
# parameters
self.has_params = True
self.params = params
# ----------- _CREATE_N_DIM_SYMB_PARAMETERS ---------- #
# ------------- MODEL DEPENDENT, IF: Model has parameters
# ------------- AND is n extendible
# ------------- If Model isn't n extendible set return to None
def _create_n_dim_symb_parameters(self):
"""Creates the symbolic parameter list for n extendible systems
:return:
pp_symb: list of sympy.symbol type entries
contains the symbolic parameters
None:
if system has a constant dimension
"""
# Create T_i are the time constants and K is the proportional factor
pp_symb = [sp.Symbol("T" + str(i)) for i in range(0, self.n)]
pp_symb = [sp.Symbol("K")] + pp_symb
return pp_symb
# ----------- SET DEFAULT INPUT FUNCTION ---------- #
# --------------- Only for non-autonomous Systems
# --------------- MODEL DEPENDENT
def uu_default_func(self):
"""
:param t:(scalar or vector) Time
:param xx_nv: (vector or array of vectors) state vector with
numerical values at time t
:return:(function with 2 args - t, xx_nv) default input function
"""
def uu_rhs(t, xx_nv):
u = 10
c = t > 0
try:
uu = list(c * u)
except TypeError:
uu = [c * u]
uu = [np.sin(0.387298334621 * t)]
return uu
return uu_rhs
# ----------- SYMBOLIC RHS FUNCTION ---------- #
# --------------- MODEL DEPENDENT
def get_rhs_symbolic(self):
"""
:return:(matrix) symbolic rhs-functions
"""
if self.dxx_dt_symb is not None:
return self.dxx_dt_symb
xx_symb = self.xx_symb
u1 = self.uu_symb[0]
K_symb = self.pp_symb[0]
TT_symb = self.pp_symb[1:]
# create symbolic rhs functions
# define entry/derivation 1 to n-1
dxx_dt = [entry for entry in xx_symb]
dxx_dt = dxx_dt[1:]
# define entry/derivation n
sum_vec = []
# write all summands of the expanded inverse laplace into a vector
for k in range(self.n + 1):
next_elem = self._create_factor(TT_symb, k)
sum_vec = sum_vec + [next_elem]
# calculate expanded inverse laplace
inv_laplace = 0
for i in range(len(sum_vec) - 1):
inv_laplace = inv_laplace + sum_vec[i] * xx_symb[i]
dxn_dt = (K_symb * u1 - inv_laplace) * 1 / sum_vec[-1]
dxx_dt = dxx_dt + [dxn_dt]
# put rhs functions into a vector
self.dxx_dt_symb = sp.Matrix(dxx_dt)
return self.dxx_dt_symb
# ----------- CREATE_FACTOR ---------- #
# --------------- Exclusivly made for this model
def _create_factor(self, pp_symb, deriv_nr):
"""Auxiliary Function to create the symb function of the pt_n element
returns the factor infront of the state, which represents the
deriv_nr-th derivation of y. Take a look at product in the equation
for dx_n_dt in the model documentation.
:param pp_symb: list of sympy variables
symbolic parameter vectorm, which only contains the time coefficients
:param deriv_nr: int >= 0
number of the state of the dxn_dt solution for which the leading factor
shall be calculated
:return summand: sympy function
returns the summand of
"""
# assure, that deriv_nr is a proper value
assert deriv_nr >= 0, "deriv_nr needs to be positive or zero"
assert deriv_nr <= len(
pp_symb
), "deriv_nr can't be greater than the \
length of the pp_symb list"
# initialize summand
factor = 0
# Solve Special case of deriv_nr = 0
if deriv_nr == 0:
factor = 1
# create factor for deriv_nr > 0
else:
# create list of all deriv_nr-element combinations
subsummand_vec = list(comb(pp_symb, deriv_nr))
# save length of the sublists, to improve performance
sublist_len = len(subsummand_vec[0])
# iterate over the combinations and create summand = sum of subsummands
for i in range(len(subsummand_vec)):
subsummand = 1
# create one summand of the factor
for j in range(sublist_len):
subsummand = subsummand * subsummand_vec[i][j]
# add subsummand to factor
factor = factor + subsummand
return factor
# -*- coding: utf-8 -*-
"""
Created on Fri Jun 11 13:51:06 2021
@author: Jonathan Rockstroh
"""
import sys
import os
import numpy as np
import sympy as sp
import tabulate as tab
model_name = "Stable_PT_n_Element"
# --------- CREATE SYMBOLIC PARAMETERS
pp_symb = [K, T1, T2] = sp.symbols("K, T1, T2", real=True)
# -------- CREATE AUXILIARY SYMBOLIC PARAMETERS
# (parameters, which shall not numerical represented in the parameter tabular)
# --------- SYMBOLIC PARAMETER FUNCTIONS
# ------------ parameter values can be constant/fixed values OR
# ------------ set in relation to other parameters (for example: a = 2*b)
# ------------ useful for a clean looking parameter table in the Documentation
K_sf = 3
T1_sf = 5
T2_sf = 0.5
# List of symbolic parameter functions
pp_sf = [K_sf, T1_sf, T2_sf]
# Set numerical values of auxiliary parameters
# List for Substitution
# -- Entries are tuples like: (independent symbolic parameter, numerical value)
pp_subs_list = []
# OPTONAL: Dictionary which defines how certain variables shall be written
# in the tabular - key: Symbolic Variable, Value: LaTeX Representation/Code
# useful for example for complex variables: {Z: r"\underline{Z}"}
latex_names = {}
# ---------- CREATE BEGIN OF LATEX TABULAR
# Define tabular Header
# DON'T CHANGE FOLLOWING ENTRIES: "Symbol", "Value"
tabular_header = ["Parameter Name", "Symbol", "Value", "Unit"]
# Define column text alignments
col_alignment = ["left", "center", "left", "center"]
# Define Entries of all columns before the Symbol-Column
# --- Entries need to be latex code
col_1 = ["Proportional Factor", "Time Constant 1", "Time Constant 2"]
# contains all lists of the columns before the "Symbol" Column
# --- Empty list, if there are no columns before the "Symbol" Column
start_columns_list = [col_1]
# Define Entries of the columns after the Value-Column
# --- Entries need to be latex code
col_4 = ["", "s", "s"]
# contains all lists of columns after the FIX ENTRIES
# --- Empty list, if there are no columns after the "Value" column
end_columns_list = [col_4]
Related Problems:
Extensive Material:
Download pdf
Result: Success.
Last Build: Checkout CI Build
Runtime: 3.8 (estimated: 10s)
Plot:

The image of the latest CI job is not available. This is a fallback image.